1. Előzmények
A Könyöksajtolás útján a nanovilágba című esettanulmányban bemutatott demonstrációs kísérlet az általam vezetett kutatócsoport néhány fiatal kollégájának érdeklődését is felkeltette, közöttük elsősorban dr. Gonda Viktorét. Ő elkészítette a könyöksajtolás folyamatának analitikus és végeselemes leírását is, amely részét képezte az Elméleti összefoglaló tanulmány készítése az ultrafinom (UFG) és a nanoszerkezetű tömbi (bulk) anyagok szemcseszerkezete és tulajdonságai közötti kapcsolatról, az ezeket az anyagokat alkotó krisztallitok közötti határok reális szerkezetéről című, K+F jelentésnek (Dunaújvárosi Főiskola, 2010.) [1]. Az irányításommal elkészült jelentésből a könyöksajtolás analitikus leírására vonatkozó részt ismertetjük, amelyet dr. Gonda Viktor (jelenleg az Óbudai Egyetem docense) készített.
Az analitikus leírás a konkrét eredményeken túlmenően jó példája annak, hogy hogyan kell egy első pillanatra bonyolultnak tűnő folyamatot képlékenységtani ismeretek alapján jellemezni. Gyakorlati szempontból is értékes az ennek az anyagnak a végén található táblázat, amely a könyöksajtoló szerszám geometriai jellemzői és a munkadarab becsült alakváltozásának mértéke közötti összefüggést jellemző adatokat tartalmazza.
2. Az ECAP során létrejövő alakváltozás meghatározása
A könyöksajtolás során nagymértékű nyíró alakváltozás jön létre a próbatestben. Ebben a fejezetben először definiáljuk a nyíró és az egyenértékű alakváltozást. Bemutatjuk az alakváltozás meghatározását analitikus módszerrel.
2.1. A nyírási alakváltozás és az egyenértékű alakváltozás definiálása
A nyírási alakváltozást az alaphosszra merőleges deformáció és az alaphossz hányadosaként definiáljuk (1. ábra), ha az alakváltozás kizárólag a nyírásból adódó torzulás.
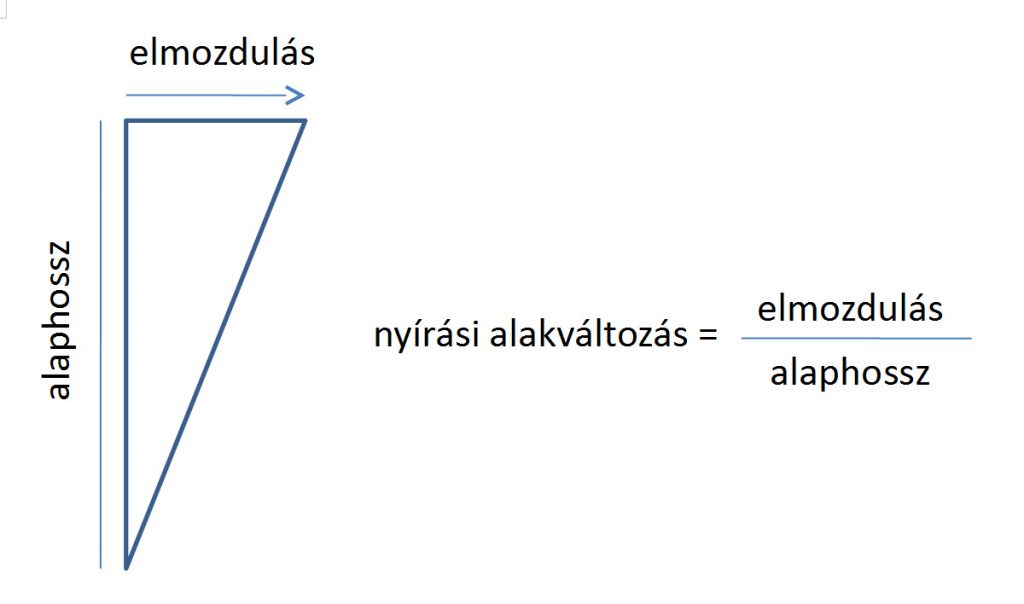
Ha egy szilárd testen az x, y, z koordinátarendszerben u, v, w elmozdulásmező adott, akkor a nyírási alakváltozás a mérnöki jelöléssel az xy síkon a test egy pontjában az alábbi alakban adható meg:
Az alakváltozás tenzoros írásmódjánál egyszerűbb a jelölés, ha ennek a felével definiáljuk a nyírási alakváltozást. Az nyírási alakváltozás tenzoros jelöléssel:
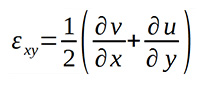Egy test alakváltozása nyírási (torzulási) és térfogati összetevőkből állhat. Az alakváltozási tenzor felírható a térfogati (volumetrikus) és a torzulási (deviációs) alakváltozások összegeként:
Ezt átrendezve, valamint a volumetrikus alakváltozást kibontva, a deviációs alakváltozási tenzor kifejezhető:
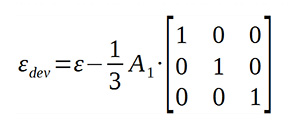ahol A1 az alakváltozási tenzor első skalár invariánsa, mely a fő alakváltozások összege:
Az egyenértékűség fogalmát könnyebb először a feszültségekkel meghatározni: egy általános feszültségállapot és egy egytengelyű (húzásnak megfelelő) feszültségállapot akkor egyenértékű, ha ugyanolyan határállapotba juttatja az anyagot. A Mohr-elmélet szerint, ez az összes terheléshez tartozó Mohr-körhöz berajzolt burkológörbe. Mivel ez a burkológörbe szerkezeti acéloknál a feszültségtengellyel párhuzamos egyenes, ezért az egyenértékű feszültséget a Mohr-kör átmérője adja (egytengelyű húzásnál ez egyenlő a maximális húzófeszültséggel). A párhuzamosságból következően az az állítás is megfogalmazható, hogy két feszültségállapot akkor egyenértékű, ha a legnagyobb csúsztatófeszültség ugyanakkora (ez a Mohr kör sugara).
A Huber-Mises-Hencky (HMH) elmélet arra a megfigyelésre alapoz, hogy alakítható anyagoknál nagy hidrosztatikus nyomásnál sem jön létre károsodási határállapot, vagyis a térfogati alakváltozási munka nem játszik szerepet. Tehát a különböző feszültségi állapotok közül azok egyenértékűek, melyeknek a torzítási energiasűrűsége egyenlő. Ugyanezt az alakváltozásokra értelmezve: két alakváltozási állapot akkor egyenértékű, ha ugyanakkora a torzítási energiasűrűsége.
A HMH egyenértékű alakváltozás a deviációs alakváltozási tenzor segítségével felírható az alábbi alakban képlékeny állapotra térfogatállandóság esetén:
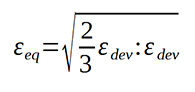
Ezt kibontva az egyenértékű alakváltozás megadható az alakváltozási összetevőkkel:
(1) 
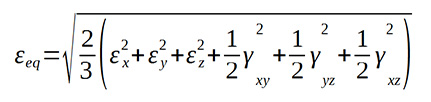
vagy a fő alakváltozásokkal is:
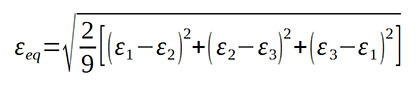Rugalmas esetre, ha az anyag összenyomható (a Poisson-tényező, ν < 0,5):
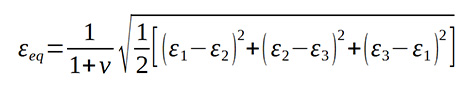
Sík alakváltozás esetén (ε3 = 0) az alábbi alakot kapjuk:
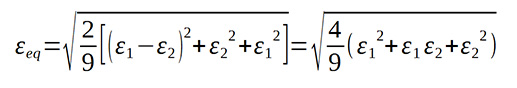
2.2. Az alakváltozás mértéke különböző könyökgeometriáknál
Az éles könyök geometriája
Könyöksajtolásnál az anyagot olyan szerszámon sajtoljuk át, mely két azonos keresztmetszetű csatornája Φ szög alatt metsződik. A Φ szög a csatornaszög. A 2. ábrán látható egy lekerekítés nélküli, „éles” könyök sematikus keresztmetszeti rajza, a csatorna szélessége a. Az átnyomás során a könyök előtti részen a kék színnel kiemelt a oldalhosszúságú T4 területű négyzet alakú anyagrész a könyök fő nyírási síkja után a kilépő oldalon látható rombusszá torzul, melynek alapja és magassága is a méretű, így területe ugyancsak T4. A rombusz dőlt oldala a csatornával Θ szöget zár be, ez a dőlésszög.
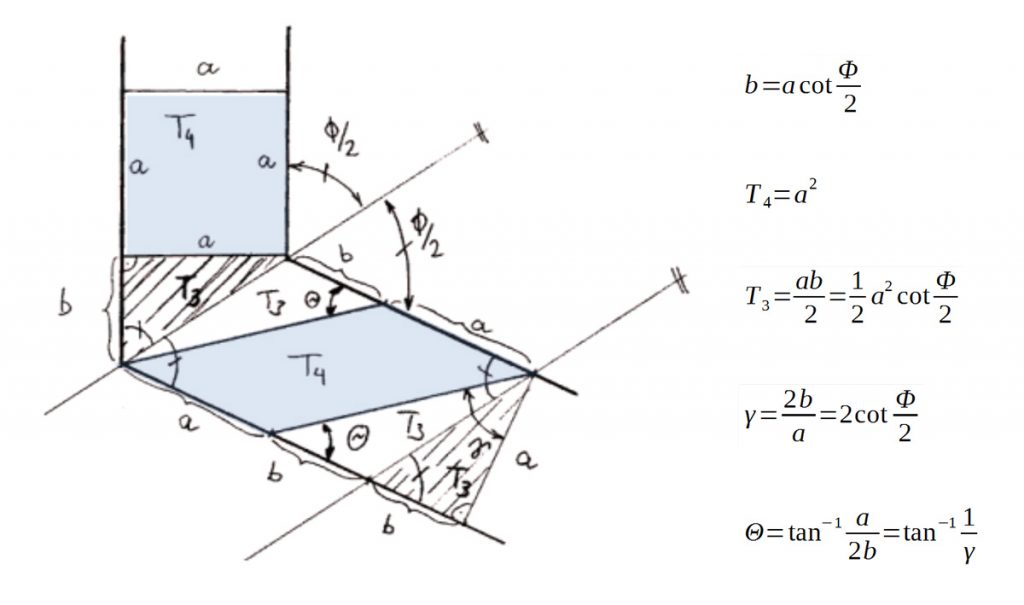
Amikor a belépő oldalon a négyzet alakú anyagrész csatorna belső oldalán levő sarka eléri a könyököt, akkor a külső oldali sarok még b távolságra van attól. Az ab befogójú derékszögű háromszög területe T3-mal jelölt. A könyökön éppen teljesen átsajtolt rombusszá torzult anyagrész egyik külső oldali sarka még épp a könyökben van, az ezen az oldalon levő belső oldali sarok a könyöktől b távolságra kell legyen, mivel az anyagáramlás állandó. A fő nyírási síkkal párhuzamost húzva a rombusz kilépő oldali sarkánál, egy ab befogójú derékszögű háromszög található, ennek területe T3. Egyszerűen bizonyítható a geometriából, hogy az a alapú rombuszt ab alapú és a nyírási síkkal párhuzamos oldalú Φ szögű rombusszá kiegészítő háromszögek területe szintén T3, de ugyanennek következnie kell a térfogatállandóságból is. A nyírási alakváltozás a 2b és a befogójú háromszögben definiálható, az ábrán γ-val jelölt. A bevezetett geometriai adatok, a nyírási alakváltozás és dőlésszög a 2. ábra jobb oldalán található képletekkel számolhatók. A nyírási alakváltozást először [Segal, 1981][2] publikálta.
2.2.1. Az egyenértékű alakváltozás becslése könyöksajtolásnál Iwahashi-módszerével
A könyöksajtolás az egyik legegyszerűbb intenzív képlékenyalakításon alapuló technika, amivel nagymértékű szemcsefinomodás létrehozható. A szemcsefinomodás, és ezáltal a szilárdságnövekedés, az átsajtolás során létrejövő nyomás alatti nagymértékű nyírási alakváltozás következménye. A létrejövő egyenértékű alakváltozás becslését [Iwahashi, 1996][3] publikálta, ez a megoldás az egyik legelfogadottabb manapság.
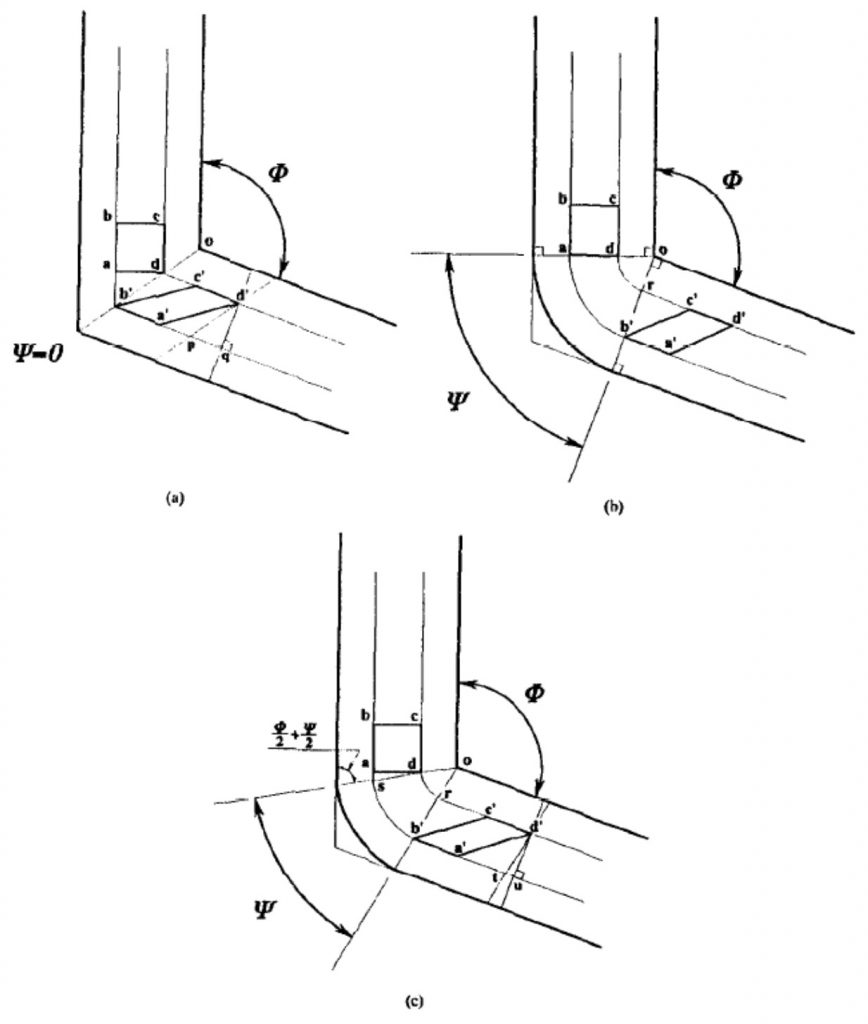
A könyöksajtolás alapelve sematikusan a 3. ábrán látható: két azonos keresztmetszetű csatorna középvonala egy adott Φ szög alatt metsződik, ez a csatornaszög. Az átsajtolás elvégezhető „éles” könyök esetén, lásd. 3(a) ábra, vagy olyan elrendezésben, ahol a könyök külső oldala lekerekített, ami a 3(b) és 3(c) ábrákon látható. Ha külső oldalon a lekerekítés szögét Ψ-vel jelöljük (könyökszög), akkor a könyökszög határértékei az éles könyöknél az 1(a) ábrán: Ψ = 0, teljesen lekerekítettnél pedig a 3(b) ábrán: Ψ = π – Φ, az 1(c) ábrán pedig egy közbenső állapotot látunk, ahol a könyökszög a két határérték között helyezkedik el.
A továbbiakban az alakváltozás meghatározásához ezt a három esetet vizsgáljuk, valamint feltételezzük, hogy az átsajtolásnál a csatorna kent, így a súrlódás elhanyagolható.
Éles könyök
Az 3(a) ábra, Ψ = 0, a minta egy kezdetben négyzet alakú elemét abcd-vel jelöltük, az átnyomás után az elnyírt alak a’b’c’d’-vel jelölt. Az 3(a) ábra jelöléseit használva a nyírási alakváltozás, γ, a következő alakban írható fel:
ahol:
- qd’ = ad vagyis a folyási irányra merőleges méret nem változik,
- a’q meghatározása pedig a geometriai vizsgálatból történhet:
- ab’ = dc’, az áramlási sebesség állandó az egyes szálakon, ez tovább egyenlő
- ab’ = dc’ = a’p = pq = ad cot (Φ/2), az ab’d háromszög és a pqd’ háromszög hasonlóságából, ezt átrendezve:
- a’q = 2ad cot (Φ/2).
Visszahelyettesítve a Ψ = 0 esetre a nyírási alakváltozásra megkapjuk a Segal-megoldást [2]:
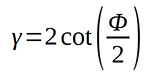
Teljesen lekerekített könyök
Az 3(b) ábrán, ahol Ψ = π – Φ, a nyírási alakváltozás a következőképpen írható fel:
ahol:
- rb’ = da = (oa – od) vagyis a folyási irányra merőleges méret nem változik,
- a’q meghatározása pedig a geometriai vizsgálatból történhet:
- ab’ = dc’, az áramlási sebesség állandó az egyes szálakon,
- ab’ = oa.Ψ = (rc’ + od.Ψ), az egyes szálakon az ívhossz, ezt átrendezve:
- rc’ = (oa – od)Ψ.
Visszahelyettesítve, a nyírási alakváltozás:
Nem teljesen lekerekített könyök
Az 3(c) ábrán, ahol 0 < Ψ < π – Φ, a nyírási alakváltozás a következőképpen írható fel:
ahol:
- d’u = ad, vagyis a folyási irányra merőleges méret nem változik,
- a’u meghatározása pedig a geometriai vizsgálatból történhet:
- a’u = a’t + tu = rc’ + as, az áramlási sebesség állandó az egyes szálakon,
- az egyes szálakon az utak:
- as = ad cot (Φ/2 + Ψ/2)
- ab’ = dc’= as + od.Ψ
- os – od = ad cosec(Φ/2 + Ψ/2), visszahelyettesítve:
- a’u = 2ad cot (Φ/2 + Ψ/2) + Ψ ad cosec(Φ/2 + Ψ/2).
Visszahelyettesítve, a nyírási alakváltozás általános alakban:
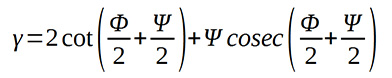Ez az egyenlet általánosan használható, az éles és teljesen lekerekített könyök peremfeltételeivel az ott levezetett nyírási alakváltozást megkapjuk.
Az egyenértékű alakváltozás, εeq egy átnyomás esetén meghatározható az 2. egyenlet alapján, ez az Iwahashi-képlet [3]:
(2)
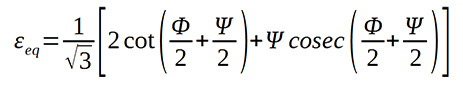Többszöri, n számú átsajtolás esetén:
(a): Ψ = 0, (b): Ψ = π – Φ, (c): 0 < Ψ < π – Φ
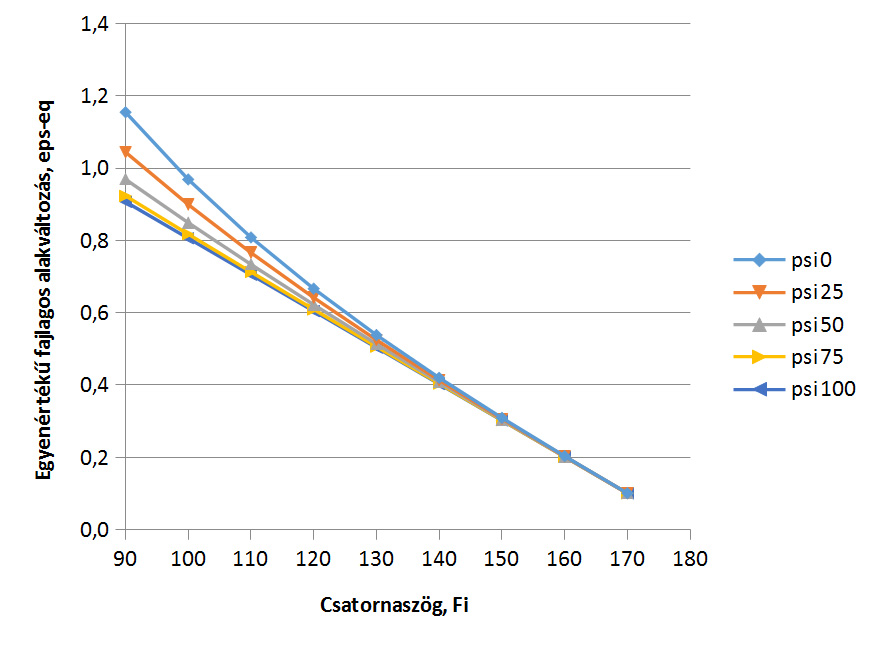
1. táblázat. Az egyenértékű alakváltozás számításához használt csatorna- és könyökszög fokban (a), egy átsajtolás esetén az egyenértékű alakváltozás (mértékegység nélkül) (b) és a létrejövő dőlésszög fokban (c).
a)
| Szögek | Csatorna | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
|---|---|---|---|---|---|---|---|---|---|---|
| könyök | psi0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| psi25 | 22.50 | 20.00 | 17.50 | 15.00 | 12.50 | 10.00 | 7.50 | 5.00 | 2.50 | |
| psi50 | 45.00 | 40.00 | 35.00 | 30.00 | 25.00 | 20.00 | 15.00 | 10.00 | 5.00 | |
| psi75 | 67.50 | 60.00 | 52.50 | 45.00 | 37.50 | 30.00 | 22.50 | 15.00 | 7.50 | |
| psi100 | 90.00 | 80.00 | 70.00 | 60.00 | 50.00 | 40.00 | 30.00 | 20.00 | 10.00 |
b)
| eps-eq | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
|---|---|---|---|---|---|---|---|---|---|
| psi0 | 1.1547 | 0.9689 | 0.8085 | 0.6667 | 0.5384 | 0.4203 | 0.3094 | 0.2036 | 0.1010 |
| psi25 | 1.1547 | 0.8994 | 0.7661 | 0.6419 | 0.5250 | 0.4137 | 0.3067 | 0.2028 | 0.1009 |
| psi50 | 0.9691 | 0.8492 | 0.7339 | 0.6224 | 0.5140 | 0.4082 | 0.3045 | 0.2022 | 0.1008 |
| psi75 | 0.9232 | 0.8175 | 0.7130 | 0.6094 | 0.5066 | 0.4045 | 0.3029 | 0.2017 | 0.1008 |
| psi100 | 0.9069 | 0.8061 | 0.7054 | 0.6046 | 0.5038 | 0.4031 | 0.3023 | 0.2015 | 0.1008 |
c)
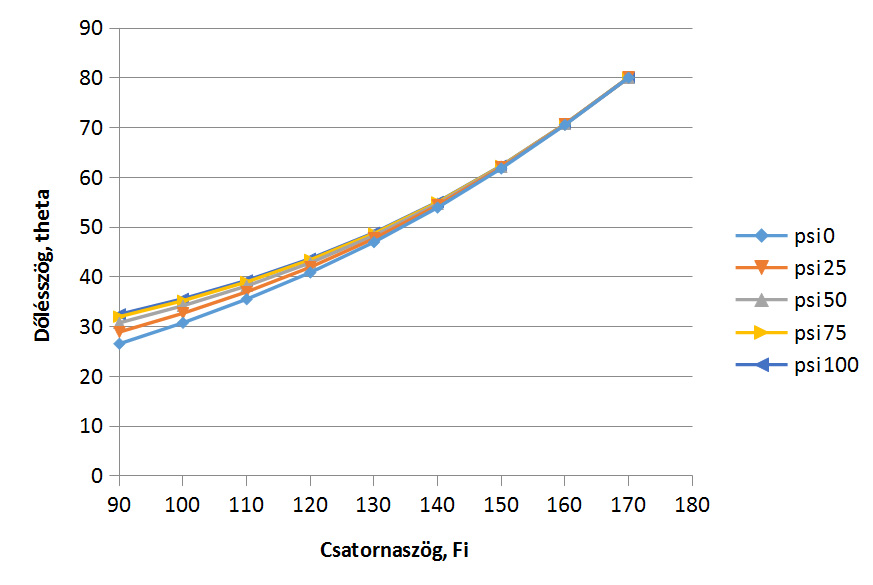
| dőlésszög | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
|---|---|---|---|---|---|---|---|---|---|
| psi0 | 26.57 | 30.79 | 35.53 | 40.89 | 47.00 | 53.95 | 61.81 | 70.57 | 80.08 |
| psi25 | 28.94 | 32.70 | 37.00 | 41.97 | 47.72 | 54.38 | 62.02 | 70.64 | 80.08 |
| psi50 | 30.78 | 34.21 | 38.19 | 42.85 | 48.32 | 54.74 | 62.19 | 70.70 | 80.09 |
| psi75 | 32.02 | 35.23 | 39.00 | 43.45 | 48.73 | 54.99 | 62.32 | 70.74 | 80.10 |
| psi100 | 32.48 | 35.61 | 39.30 | 43.69 | 48.89 | 55.08 | 62.36 | 70.76 | 80.10 |
Az egyenértékű alakváltozást az 1. táblázatban szereplő szögekre számítottuk ki. Az eredményeket a 4.a ábrán ábrázoltuk a csatornaszög függvényében egy átsajtolásra. Minél kisebb a csatorna szöge, annál nagyobb alakváltozás érhető el egy lépésben. Derékszög esetén az elérhető egyenértékű alakváltozás 0,9 teljesen lekerekített könyöknél, és közel 1,2 éles könyöknél.
A dőlésszöget, θ-t a kilépő oldalon az átnyomott próbatestnek a vízszintes csatornafallal bezárt szögével értelmezzük és a
(3)
képlettel számoltuk, és a 4.b ábrán látható a csatornaszög függvényében. Derékszögű csatornában a létrejövő dőlés 27-32 fok a könyökszög függvényében.
a)
b)
Lekerekített könyök belső rádiusszal
Az előző megoldásokban a belső rádiusz mindig zérus volt, azonban érdemes megvizsgálni azt az esetet, ha a csatorna belső oldalán is lekerekítés található, ugyanis ha a csatorna kimunkálása marással történik, akkor ez a geometria adódik. Ennek megfelelően azt az esetet vizsgáljuk, amikor a belső rádiusz rb, és a csatorna keresztmetszetének mérete a, így a külső rádiusz rb + a. A nyírási alakváltozás meghatározásához meg kell határoznunk, hogy a belső oldalon mennyivel „siet” az anyag, ezt az előzőekben b-vel jelöltük. Ezt számíthatjuk a könyök belső és külső oldalán az ívhosszak különbségével. Derékszögű csatornák esetén a belső és a külső oldalon az ívhossz:
Az ívhosszak különbsége felírható az alábbi alakban:
amiből látszik, hogy az független a belső átmérőtől, így a nyírási alakváltozás
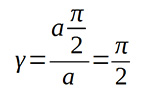is független attól, és ennek mértéke megegyezik a belső rádiusz nélküli teljesen lekerekített csatornában létrejövő alakváltozás mértékével, valamint a dőlésszögek is megegyeznek:
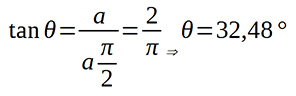Érdemes megjegyezni, hogy legkoncentráltabb a deformációs zóna az éles könyökben – elméletileg egy sík: itt tisztán nyíró az igénybevétel. A könyök lekerekítésével a deformációs zóna legyezőszerűen kinyílik, így itt az igénybevétel is összetett lesz: a nyírás mellett a hajlítás is megjelenik.
Hivatkozások
[1] Verő Balázs, szerk: Elméleti összefoglaló tanulmány készítése az ultrafinom (UFG) és a nanoszerkezetű tömbi (bulk) anyagok szemcseszerkezete és tulajdonságai közötti kapcsolatról, az ezeket az anyagokat alkotó krisztallitok közötti határok reális szerkezetéről, K+F jelentés, Dunaújvárosi Főiskola, 2010.
[2] V.M. Segal, V.I. Reznikov, A.E. Drobyshevskiy, V.I. Kopylov, Russian Metallurgy, (Eng. Transl.), 1, p. 115, 1981.
[3] Y. Iwahashi, J. Wang, Z. Horita, M. Nemoto, T. Langdon: Principle of equal-channel angular pressing for the processing of ultra-fine grained materials. Scripta Materialia, Vol. 35, No. 2, pp. 143-146, 1996.